
Backstory
A while back, my friend expressed interest in learning how to program – specifically Python. He was also in the process of saving up for a new gaming PC that he would build himself. To make learning more fun for him, I told him that I would make him custom challenges that would teach him and keep him entertained. On top of this, to motivate him to learn, I would pay for half of a computer part for each challenge he completed. All in all, these challenges added up to a decent sum of money.
My friend gave up before even completing one! So I’ve decided to not let my work go to waste, and to open the challenges up to the internet. And because I love the Vim text editor so much, I’ve decided to donate the $300 to ICCF Holland to help children in Uganda!

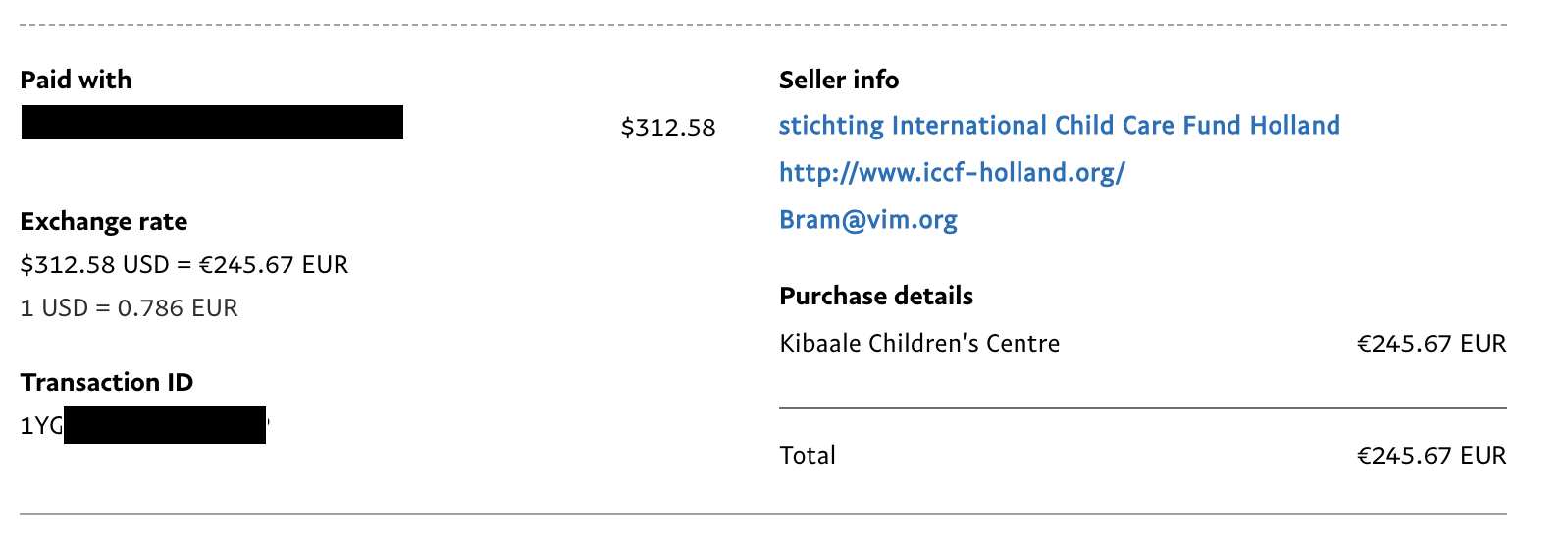
All the challenges are solvable. The pseudocode I have written will likely help you a lot, depending on your ability level. These are intermediate level programming challenges, so you should have a solid grasp of the basics first. You will not need any 3rd party libraries. By the time you finish these challenges, you’ll hopefully have grown quite a strong foundation!
Reference
- Online Python Interpreter - https://repl.it/languages/python3 (Works with Tkinter!). It will probably be better to install directly to your computer, though, from python.org
- Python official docs - https://docs.python.org/3/tutorial/. Great for reference.
- https://www.codecademy.com/ is a great resource for learning the fundamentals. Only the older version of python is free, but it is still very relevant.
- Python’s built in
help()function will also be very helpful to you! Example:help(list). Press j or k to scroll, and q to exit.
Table of contents:
- Interest Calculator
- Difficulty: 0.5
- ROT13 Cipher
- Difficulty: 1.0
- Rocket Recursion
- Difficulty: 2.0
- Project Euler Knockoff
- Difficulty 2.5
- Planet Simulator
- Difficulty 3.0
Problem 1: Interest Calculator
Difficulty: 0.5
After 25 years of saving cash in your bank account and letting it inflate away, you finally think you understand compound interest and decide to invest in the S&P 500! To test your skills, you will make a compound interest calculator. It will take user input, and calculate a return on investment after a certain number of years.
- COMPOUND INTEREST – https://en.wikipedia.org/wiki/Compound_interest
Use the formula: $$P^\prime = P\left(1 + \frac{r}{n}\right)^{nt}$$ where
- P is the original principal sum
- P’ is the new principal sum
- r is the annual interest rate (convert from percent to decimal)
- t is the overall length of time the interest is applied (years).
- Pseudocode:
- 1_interest_calculator_pseudocode.py
Knowledge Prerequisites:
- Variables, Math operators: +, -, *, /, ** where ** means ^ (power), order of operations, print()
Completeness Criteria:
- Variables, Math operators: +, -, *, /, ** where ** means ^ (power), order of operations, print()
- Find new principal on $5000 at 15% interest for 10 years, compounded once a year.
- Should be equal to 2xxxx.xx
- Find new principal on $5000 at 15% interest for 10 years, compounded quarterly.
- Should be equal to 2xxxx.xx
- Use the pseudocode, unless you come up with a better method, or wish to try something different
- Explain your code.
- Solution:
- 1_interest_calculator.py
Problem 2: ROT13 Cipher
Difficulty: 1.0
You’re an intern working at a classified government military base. You have been tasked by the five star general to develop a new type of cipher for communicating securely with nuclear submarines in enemy territory.
After a discreet wikipedia search, you learn that a cipher is an algorithm for performing encryption and decryption. You decide to impress the general by your new ‘invention’ that you neglected to notice already exists on the wiki: a ROT13 cipher. ROT13 works by shifting to the next 13 letters in the alphabet, you explain. Encoding and decoding a string uses the same function. For example, “secret” → “frperg” → “secret”
Don’t worry about encrypting numbers/special characters (or anything that isn’t in the lower case alphabet, for that matter).
- Pseudocode:
- 2_rot13_pseudocode.py
Knowledge Prerequisites:
- ROT13, input(), string.lower(), print(), strings, for loop, string.find(), for, if/else statement, == operator, + operator, modulo
Completeness Criteria:
- Encrypt “the quick brown fox jumped over the lazy dog”
- Copy the output from above and encrypt it again. You should be right back where you started.
- Use the pseudocode, unless you come up with a better method, or wish to try something different
- Explain your code. You must not use the codecs module, this is cheating.
- Solution:
- 2_rot13.py
Problem 3: Rocket Recursion
Difficulty: 2.0
You’re a soviet rocket engineer still working on the crewed moon landing from the space race in the 60s. You are tasked with designing a rocket that can make it all the way to the moon, and need to write a recursive program to estimate the approximate wet launch mass of the final rocket. This is a good introduction to the Functional programming style.
Rockets work in a certain way where a greater energy corresponds to exponentially more fuel. This is why the massive Saturn V rocket was needed to deliver the tiny moon lander. Naturally, you will split your rocket up into 3 stages – this way, you won’t be lugging massive empty tanks to the moon. You will be using the Tsiolkovsky rocket equation. Keep in mind you will have to use the rocket equation 3 times – once for each stage.
- ROCKET EQUATION – https://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation
The rocket equation is defined by: $$\Delta v = v_e\ln \left(\frac{m_o}{m_f} \right)$$ where:
- Δv = change in velocity (km/s)
- v_e = exhaust velocity (km/s)
- m_o = initial total mass / wet mass (kg)
- m_f = mass without propellant / dry mass (kg)
It can be rearranged to: $$m_o = m_f \cdot e^{\frac{\Delta v}{v_e}}$$
Here is your flight itinerary (don’t lose it!):
| Stage | dv | v_e | m_f |
|---|---|---|---|
| 1: Earth Surface to Low Earth Orbit | 9.4 km/s | 2.3 km/s | 16000 kg |
| 2: Low Earth Orbit to Moon Capture | 3.26 km/s | 2.3 km/s | 8000 kg |
| 3: Moon capture to Moon Surface | 2.41 km/s | 2.3 km/s | 4500 kg |
NOTES:
- Keep in mind that the dry mass after a burn is equal to the dry mass of the stage that you just burned, PLUS the wet mass of all further stages.
- For credit, you must use a recursive solution. Refer to the pseudocode.
- HINT: Pass the first item in the list into the function to solve for the first stage, then recur but only pass the rest of the values into the recursion
Also, don’t worry about getting the astronauts back – the space program doesn’t have the budget for that.
- Pseudocode:
- 3_rocket_recursion_pseudocode.py
Knowledge Prerequisites:
- Functions, return, recursion, lists, dictionaries, math.exp(), dict.get(), list indexing, print(), high school algebra, f strings
Completeness Criteria:
- Implement a recursive solution
- Use the pseudocode, unless you come up with a better method, or wish to try something different
- Explain your code
- Ending value is equal to 607xxxx.xx kg, print it out to two decimal points
- Solution:
- 3_rocket_recursion.py
Problem 4: Project Euler Knockoff
Difficulty: 2.5
This project was written in the likeliness of projecteuler.net. It’s a cool website that challenges you with a bunch of problems similar to this one. When you solve each problem, you get admitted to a secret club where people discuss how they solved it.
A fibonacci prime is a prime number that also lies in the fibonacci sequence. Find the 12th Fibonacci prime. It might take your computer a minute or two, it’s a big number! However, if it takes you more than 2 minutes, there’s definitely a better solution. Also, for some reason, google lists fibonacci primes that aren’t actually prime numbers – so don’t google a solution!
- Pseudocode:
- 4_project_euler_knockoff_psudocode.py
Knowledge Prerequisites:
- Functions, return, Generator functions, yield, prime numbers, fibonacci sequence, while loop, if/else, for, range(), math.ceil(), math.sqrt(), modulo, while loop, list.append(), next()
Completeness Criteria:
- Output must follow the sequence 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, …
- Number must be equal to 99194853094xxxxxx
- Use the pseudocode, unless you come up with a better method, or wish to try something different
- Explain your code.
- Solution:
- 4_project_euler_knockoff.py
Problem 5: Planet Simulator
Difficulty: 3
Common thought is that planets actually revolve around the sun. Your goal is to visualize this behavior, in a (more or less) scientifically accurate manner. You are to write a simulator library that predicts orbits in a graphical environment, using tkinter (Python’s native Graphical User Interface module). This is a good introduction to the Object Oriented Programming style. Your simulation should look like this by the time you have finished:
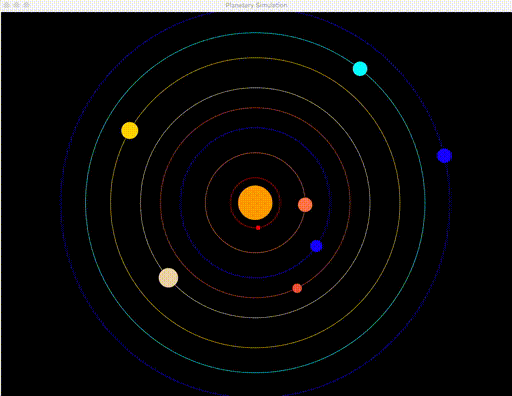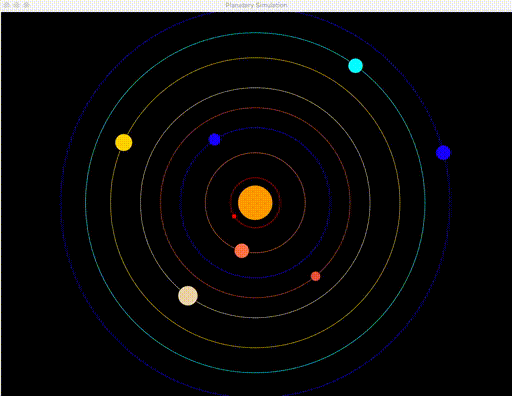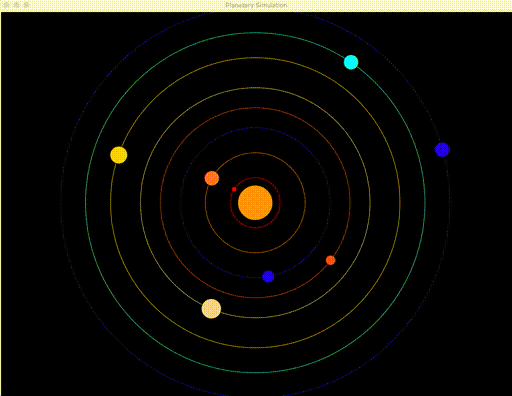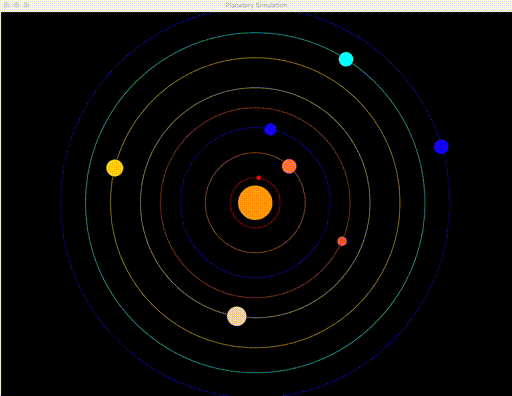
Create a simulation for: The Sun, Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune. All planets should revolve around the sun, where each second corresponds to 80 earth days. Relative movement speeds should be scientifically accurate – refer to the data given. The simulation can start with all planets in a straight line, or in random positions – both are acceptable.
NOTES:
- Do not worry so much about drawing the simulation to scale, as that would be near impossible. Just make sure the big planets are big, and the small planets are small.
- Assume all orbits are perfect circles.
- Color each planet with a fitting color, and same-color orbit path.
- HINT: use the Unit Circle from high school algebra to solve for planet positions with respect to time. Remember cos() and sin().
- Bonus points if you can bind a quickkey to exit the program (like “q”)
Finally: Pluto is not a planet. Solutions with pluto will not be accepted. Just kidding, you can add it if you really want to.
You are supplied with the following data for each planet’s period:
| Planet | Period |
|---|---|
| Mercury | 87.97 days |
| Venus | 224.7 days |
| Earth | 365.3 days |
| Mars | 686.93 days |
| Jupiter | 11.86 years |
| Saturn | 29.42 years |
| Uranus | 83.75 years |
| Neptune | 163.72 years |
- Pseudocode:
- 5_planet_simulator_pseudocode.py
Knowledge Prerequisites:
- High School Algebra (Unit Circle), tkinter, math.cos(), math.sin(), time.time(), random.random(), Python Classes, instance variables, tuples, tkinter.Tk.resizable(), tkinter.Tk.title(), tkinter.Tk.bind(), tkinter.Canvas(), tkinter.Canvas.pack(), python dictionaries, tkinter.Canvas.create_oval(), dict.update(), tkinter.Canvas.after(), tkinter.mainloop(), if __name__ == ‘main’: main()
Completeness Criteria:
- Simulation must have a black background, all 8 planets + the sun must be shown, with slightly different size planet sizes and orbit radii. The sun must not move.
- Planet orbit periods must be scientifically accurate. That means that earth must rotate almost twice as fast as mars, etc.
- Use the pseudocode, unless you come up with a better method, or wish to try something different.
- Explain your code
- Solution:
- 5_planet_simulator.py